LSM Trees, Memtables & Sorted String Tables: An Introduction

If you keep things tidily ordered, you're just too lazy to go searching.

-German Proverb

In this blog post, I will outline what LSM Trees, memtables, and Sorted String Tables (SSTables) are. The reason for this explanation is twofold:

1. I am currently (though admittedly not consistently enough) working on my own implementation of a database storage engine, particularly an LSMT version. It is similar to this Harvard graduate course project, but I am going to go beyond the single node implementation and load test a distributed version. So this post can serve as possibly one of many in a series of posts about the venture. The plan is to implement the storage engine, then the auxiliary components of the DB implementation, and finally to distributed concerns such as leader election, replication, read repair, etc. Very exciting, I know!
2. I am hoping that writing this out can serve as an aid to my own understanding, forcing me to fill in any gaps in my knowledge as I go along. I expect that if I revisit this post a year from now, I might laugh at how little I truly knew!

So to start, LSM Tree stands for Log-Structured Merge-Tree. The name comes from the paper by Patrick O'Neil and Edward Cheng called "The Log Structured Merge Tree", which itself found inspiration from the log structured filesystem paper by Rosenblum and Ousterhout. The LSM Tree design is an alternative to the B tree (and variants) centered strategy used in a lot of other storage engines such as innodb (MySQL/MariaDB) and PostgreSQL. While a B tree must be updated in place on disk (or subtrees copied and replaced), the LSM Tree can write data sequentially while still keeping data in sorted order.  This optimizes write throughput by not needing to write in place like a B tree, as well as avoiding complex latching mechanisms (although this process is being improved upon). How is this achieved?

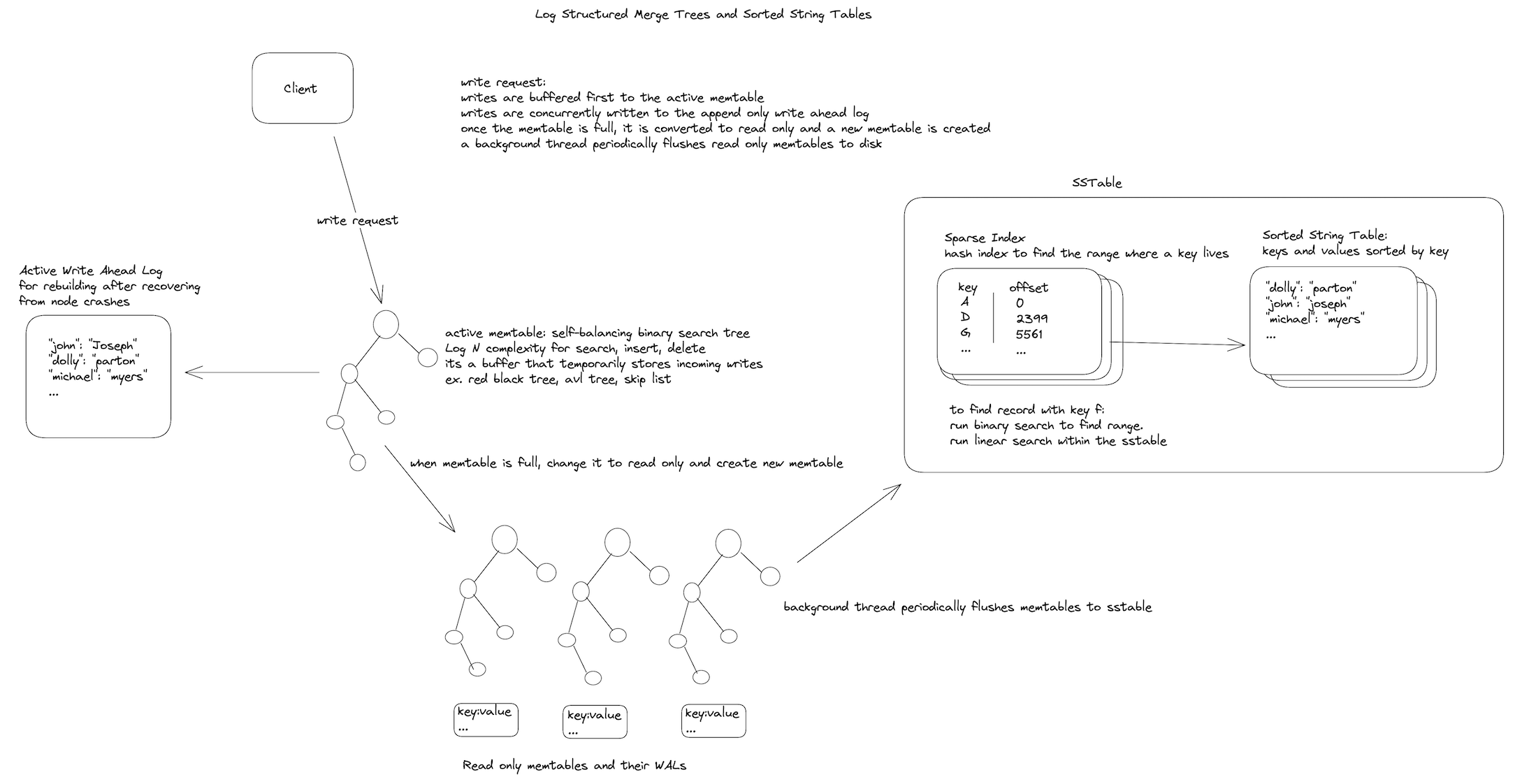
tl;dr: Writes come first to an in-memory logarithmic insert data structure (like a skip list) and simultaneously to a write ahead log for durability. After the in-memory table is too big, it is retired to read-only (while another memtable is promoted for writing atomically) and eventually flushed in its entirety to an on-disk component called a Sorted String Table. It's called this because the data is sorted. It is maintained sorted in memory and written from top to bottom to disk. This way we can conveniently compact and merge the on disk tables over time in sorted order in a type of merge sort procedure. See the write and read path images at the bottom of this post.

In sorted LSM Trees (there are also unsorted, or insertion-order LSM Trees), writes are first appended (buffered) to an in-memory sorted data structure. There are no deletions per se to this data structure, just additions. Any deletion would come in the form of a tombstone, that is, setting the value specifically to a delete value instead of removing it. This avoids "resurrecting" a previous value. For example if a key "bob" is set to 1 in a SSTable, and then simply removed in an in-memory table, the resulting flush would not have that value. As a result, any read would eventually reach the older SSTable and return the previous value. Instead you want to mark that key with a special tombstone value so that any read would know it is removed. Eventually through compaction (a deep dive into compaction strategies will be in another blog post) the outdated value will be removed.

This in-memory data structure is sometimes called a memtable (as in memory table; the words memtable and SSTable originally came from the Google Bigtable paper), and the actual implementation can vary. It can be a self-balancing binary search tree such as a Red-Black Tree or an AVL Tree. It seems that many modern databases implement the memtable as a skip list, which although does not have deterministic balancing still is likely to be balanced due to the nature of its probabilistic insertions. It seems that a skip list may be preferable due to its comparatively simple implementation and concurrent access. It's a pretty cool data structure. Of course, it's the balanced nature of these structures that limits length to logarithmic height and Big-O(log(n)) insertion, deletion, etc.

It should be noted that in many implementations the memtable is flushed to disk in batches, and multiple memtables can be maintained for concurrent reads. Usually only one memtable is available for writes and once full is turned immutable for reads only while a new memtable takes its place. This reduces the frequency of flushes and minimizes the potential for performance bottlenecks. All SSTables are immutable and ready only.

In practice, there can be a mixture of data structures. RocksDB by default uses a skip list but also implements a hash link list, hash skip list, and a vector. Apache Cassandra implements skip lists and interestingly a Trie memtable also. I read this fantastic paper on it (Trie Memtables in Cassandra) that goes in depth on the optimizations provided by this data structure, specifically for Cassandra and the JVM. CockroachDB uses the Pebble storage engine which is based on RocksDB and implements its memtable as a skip list. HBase also implements its own memstore as a skip list. Safe to say that a skip list is a must know data structure if you are looking to implement your own storage engine. The variations that these different databases use is worthy of a blog post of its own and a deep dive into the trade-offs for particular data structures is well worth it. That will most likely be my next blog post on this subject, along with implementing the memtable in C++.

At the same time that writes are written to this in-memory data structure in sorted order, writes are also appended in insertion order to an append only write ahead log. This is mostly a durability measure. In the case of an unexpected failure, the memtable(s) would be lost. On startup the node has to reconstruct the memtable(s) from the log. In Cassandra the write ahead log (called a CommitLog) keeps track of "active" segments of the log that need to be reconstructed, along with the "allocating" segment that is used for active writes. So incoming writes are written to this allocating segment, then once that log becomes to large a new one is used for writes. As soon as the corresponding memtables for the log entries are flushed to disk the log segment for it can be discarded. This whole process is deserving of it's own blog post and implementation deep dive.

Finally the on-disk component of the LSM Tree is the Sorted String Table. In order to write the contents of a sorted data structure, whether a tree, skip list, vector, or any other data structure, you just need to iterate in order from the lowest value to the highest. So it is a very simple and straightforward linear operation. It should be noted that the original O'Neil/Cheng paper describes two different LSM Tree designs. One is the two-component LSM Tree and another is the multi-component LSM Tree. The difference is that in the two-component design there is only one table on disk (not several SSTables, just one) implemented as a b-tree, and so writes follow a copy-on-write design where the entire identified subtree is copied and then modified, and only when all the changes are done is the top most pointer to that subtree atomically updated. In this design the writes are immutable in the sense that changes are only done on copies, so concurrent readers need not worry about seeing mixed results. Alex Petrov, in his gripping book "Database Internals" mentions that he does not know of any two-component implementations. I do not either. The multi-component LSM Tree is the more popular version, and includes several SSTables. Each memtable when flushed becomes it's own SSTable, which are then compacted and merged later on asynchronously.

The LevelDB implementation is simple and clear in the DBImpl::WriteLevel0Table and the BuildTable methods. The "Level0" part of the function name will make more sense when we discuss compaction strategies. For now it is enough to know that level 0 is simply the first iteration of SSTable, where no guarantee is made about the overlapping of keys. In other words, it's just whatever the memtable was at that time flushed to disk. Later on during compaction there can be guarantees such that the SSTable keys don't overlap with each other. The memtable is flushed when it reaches a certain configurable size. In RocksDB this configuration key is called write_buffer_size. As you can see RocksDB allows multiple memtables to exist in memory before they are flushed, although only one is used for writing at a time. From the RocksDB wiki:

Flush

There are three scenarios where memtable flush can be triggered:

1. Memtable size exceeds ColumnFamilyOptions::write_buffer_size after a write.

2. Total memtable size across all column families exceeds DBOptions::db_write_buffer_size, or DBOptions::write_buffer_manager signals a flush. In this scenario the largest memtable will be flushed.

3. Total WAL file size exceeds DBOptions::max_total_wal_size. In this scenario the memtable with the oldest data will be flushed, in order to allow the WAL file with data from this memtable to be purged.

As a result, a memtable can be flushed before it is full. This is one reason the generated SST file can be smaller than the corresponding memtable. Compression is another factor to make SST file smaller than corresponding memtable, since data in memtable is uncompressed.

The Sorted String Table (SSTable for short) is simply a file with data entries where the keys are in sorted order. There is also usually an index file either implemented as a B tree or a hash table. Along with the key and value are certain metadata such as the size of the data, in order to know how much space to skip to get to the next entry. This is essential because the entries are not all of uniform size and therefore there is no way to reliably perform a binary search on the sorted data. To actually find the key you are looking for when reading from an SSTable, there must be an index to tell you where certain keys are. This can be in the form of a sparse index hash table, which will tell you the location of a key directly. Then you can linearly search from there. For example if you are looking for a key "bob" and the sparse index has the keys "alice" at position 0 and "david" at position 800, then you know "bob" must be in between them. Of course in a B tree index, the search for a key is directly logarithmic.

Key to the LSM Tree design is the idea of merging and compaction. Over time the SSTables become fragmented and older entries take up a lot of space. What if you never merged or compacted these files? Then for every read you would have to go further and further back to get a key that perhaps was only written once ten years ago. So the SSTable that holds this key/value is from 100 on disk files ago, and a read for it first searches the memtables then sequentially each written table (let's ignore bloom filters for now). This problem is called read amplification, where one read query results in many read operations. This is also a form of space amplification, where if we have obsolete data in our SSTables, we keep it for a very long time. Imagine if we had one key dominate our database with updated values all the time, all of our SSTables would probably have a version of this key although we would only need one (the last one)!

The solution is to run a sort of merge sort on the files, first by taking the lowest key from each SSTable and creating a new entry in a new, compacted SSTable. Imagine you have an iterator that can move through every entry linearly of an SSTable. Now imagine you have a pointer to the heads of multiple iterators, each one corresponding to an on disk file. The value of each head can then just go into a priority queue such as a min-heap. The priority queue will tell you which is the smallest value, which you can pop and place into the new SSTable. Once a value is removed from the priority queue you can update the iterator for it and place its next value in the priority queue. Once an iterator is exhausted you can simply ignore it. The values are overwritten so that only the latest value from the key (from all the files at hand) is memorialized in the newly formed table. If you had a priority queue all with the same key, you would have to reconcile the records by looking at the metadata of the SSTable, which would include a timestamp. So only the key with the highest timestamp would be considered the final value.

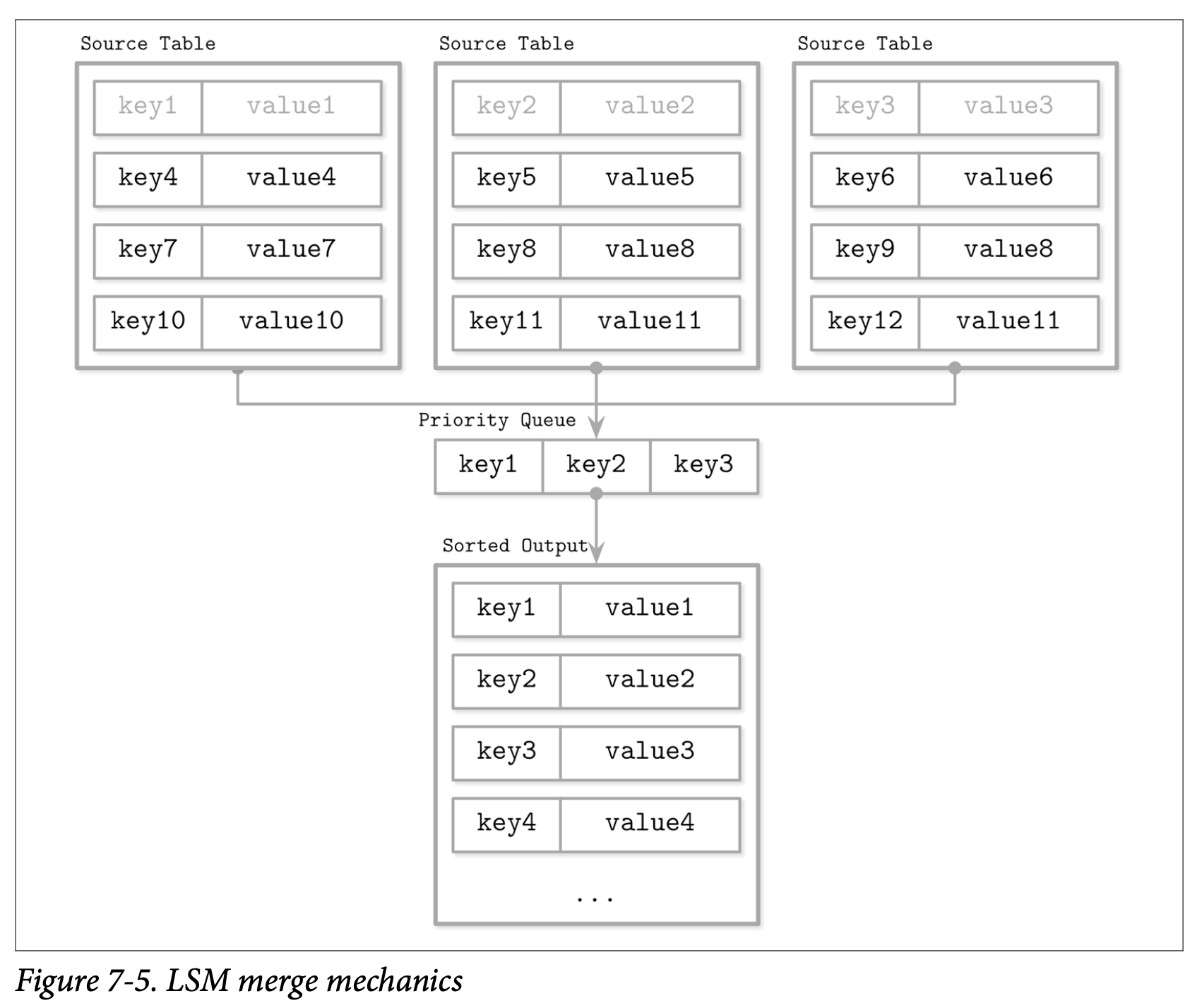
One issue is that it is possible to cause write amplification by re-writing the same value over and over again. So even though we have one key with one value, due to compaction we end up re-writing it in different files over time. That is why there are different compaction algorithms to deal with this and optimize for different approaches. Some of these compaction strategies are size-tiered compaction, leveled compaction, time window compaction, and others. This is a very big topic that definitely deserves its own blog post.

Finally, the high level algorithm for LSM Tree storage engines are clear.

• First, all incoming writes update in the memtable, which is an in-memory self-balancing binary tree or skip list or similar structure, and the Write Ahead Log. There can be more than one memtable for reading before flushing but only one for writing.
• Once the memtable reaches a configurable size alone or as a whole amongst all memtables or when the WAL is too large, it is flushed in the form of a SSTable to disk. Usually the memtable flushed is not the same memtable being used for active writes, still, reads will switch away from the memtable and to the SSTable atomically.
• The SSTables on disk are periodically compacted and merged together to save disk space and ease data fragmentation.
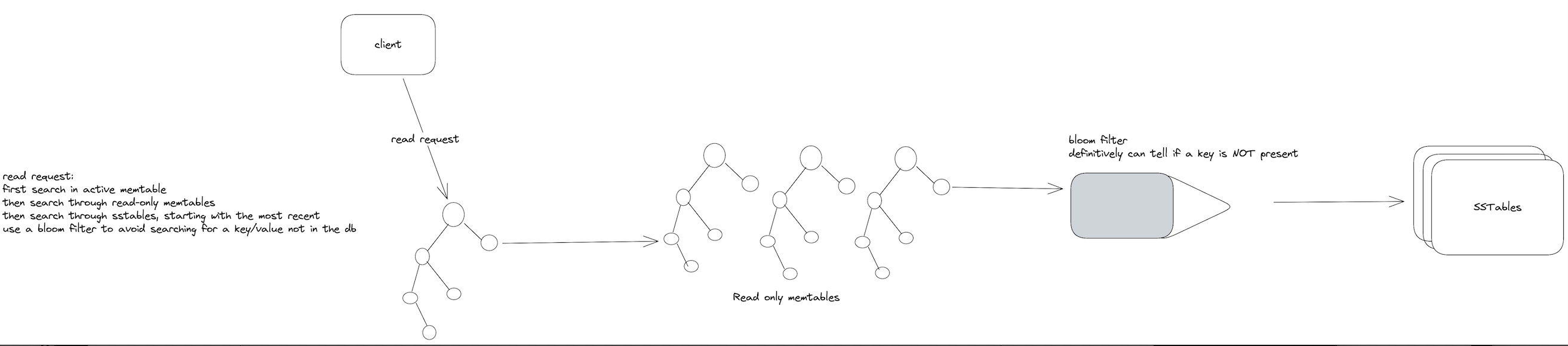
• Read requests first check in the in-memory structures and only then begin searching through SSTables beginning from newest to oldest.

Here is a pictorial representation of the write path generally speaking of the LSM Tree design (there can be varied optimizations across different database designs):

Many LSM Tree storage engines utilize bloom filters to avoid having to waste disk reads looking for a key that doesn't exist in the database. A bloom filter can definitively say whether a key is NOT in a set. It may have false positives but that is an acceptable tradeoff to avoid read amplification on queries that are most definitely not available, as that would require reading all the tables in the database. Cassandra employs a bloom filter as does RocksDB.

Here is a drawing for the read path:
 

For now, I will end with this. The work ahead is cut out for me. I need to deep dive into every area of this strategy piecemeal in order to write my own implementation. So far the biggest areas are:

• memtable implementation and data structure trade-off discussion (skip list, red-black tree, etc.)
• write-ahead log and implementation
• SSTable on disk file representation and compression
• Compaction strategy differences and trade-offs, merge sort of SSTables
• Bloom filter implementation

Until next time!